[RMMV] HELP WITH STAT/FORMULA BALANCE!
Posts
Pages:
1
So, I'm now working in the formulas for my game, Dreameerie. The thing we have right now is that characters don't increase in stats passively by level up, instead we give stats through quest completion (choices may affect which stats are gained), consumables scattered around dungeons and through upgrades on equipment.
In combat, the stats we use beyond Mana and HP are:
-Strength -> affects ALL basic attacks and Red abilities*
-Dexterity -> affects all Green abilities in addition to crit and dodge chance.
-Magick -> affects all Blue abilities (we'll add some more things here in the future)
-Physique -> reduces all damage.
-Recovery -> affects heals, lifesteal and such.
-Speed -> affects turn order and escape chance.
(RED, GREEN and BLUE abilities are those of 6 elemental properties which are used by all damaging abilities and weapon attacks. Each main stat is tied with two of those elements.)
However, we're a little worried about how to balance this out. So far our damage formulas are simple a.atk - b.def kind of stuff (we're still balancing the first dungeon) and we were considering perhaps using a different system. Something in which every ability has a base damage component which is only increased through stats, such as (60 + (a.mat * 0.75)) - b.def.
What do? Would using base damage for stuff easier to balance? What would you consider the best way to balance combat for the whole game?
Also, any other games which use a similar stat system and succeeded? I don't really know any.
In combat, the stats we use beyond Mana and HP are:
-Strength -> affects ALL basic attacks and Red abilities*
-Dexterity -> affects all Green abilities in addition to crit and dodge chance.
-Magick -> affects all Blue abilities (we'll add some more things here in the future)
-Physique -> reduces all damage.
-Recovery -> affects heals, lifesteal and such.
-Speed -> affects turn order and escape chance.
(RED, GREEN and BLUE abilities are those of 6 elemental properties which are used by all damaging abilities and weapon attacks. Each main stat is tied with two of those elements.)
However, we're a little worried about how to balance this out. So far our damage formulas are simple a.atk - b.def kind of stuff (we're still balancing the first dungeon) and we were considering perhaps using a different system. Something in which every ability has a base damage component which is only increased through stats, such as (60 + (a.mat * 0.75)) - b.def.
What do? Would using base damage for stuff easier to balance? What would you consider the best way to balance combat for the whole game?
Also, any other games which use a similar stat system and succeeded? I don't really know any.
Making each stat equally useful is something you can only really perfectly balance by testing your game.
On the other hand, does the player even have a choice on what stat to increase? If not, then it doesn't really matter that much, does it?
I'd say the formula you use doesn't really matter in terms of balancing, because there are actually variables you can modify as well. Like if the attack stats are simply 60 higher than the defense stats and you just put ATK-DEF as formula, you end up with 60 damage just like you would if all stats are the same and you put 60+ATK-DEF as formula.
Putting skill damage formulas is more a matter of how you want your skills to be like. Should they always be useful from start to finish? Should they get gradually less useful until they are replaced by a stronger version of the spell?
Usually I'd put down the formulas first based on how I want the skills to be and do the actual balancing when it comes to player and monster stats instead. It's more flexible than finding that one perfect formula that works from start to finished based on your character progression system.
On the other hand, does the player even have a choice on what stat to increase? If not, then it doesn't really matter that much, does it?
I'd say the formula you use doesn't really matter in terms of balancing, because there are actually variables you can modify as well. Like if the attack stats are simply 60 higher than the defense stats and you just put ATK-DEF as formula, you end up with 60 damage just like you would if all stats are the same and you put 60+ATK-DEF as formula.
Putting skill damage formulas is more a matter of how you want your skills to be like. Should they always be useful from start to finish? Should they get gradually less useful until they are replaced by a stronger version of the spell?
Usually I'd put down the formulas first based on how I want the skills to be and do the actual balancing when it comes to player and monster stats instead. It's more flexible than finding that one perfect formula that works from start to finished based on your character progression system.
Well, if stats only go up by completing quests, you might consider making certain quests improve certain stats as a method for players to tailor their characters. If they all go up, that's probably fine too.
I think the question in regards to game-balance becomes how much stats go up, and exactly how many of these quests are mandatory. Though, it might be possible some quests aren't available until later in the game (after certain other mandatory quests are done?), so, that might be something to keep in mind as well.
I think the question in regards to game-balance becomes how much stats go up, and exactly how many of these quests are mandatory. Though, it might be possible some quests aren't available until later in the game (after certain other mandatory quests are done?), so, that might be something to keep in mind as well.
LockeZ

I'd really like to get rid of LockeZ. His play style is way too unpredictable. He's always like this too. If he ran a country, he'd just kill and imprison people at random until crime stopped.
5958
There are two basic categories of damage formulas - subtractive defense and divisive defense.
Subtractive defense is the kind you're using now. The target's defense, or some number based on their defense, such as sqrt(defense), is subtracted from the final damage.
Divisive defense is when the final damage is divided by some number based on the target's defense. For example, (a.atk * 10 / b.def) is a simple and common divisive damage formula.
The main difference between these two types of formulas is whether having high enough defense can cause an attacker to do 0 damage. In certain types of games, it may be desirable to use a subtractive formula for this reason, for example in games where HP is low and healing is difficult but positioning or elemental defense is used to prevent damage. It may also be desirable in games with a very strong focus on using the right element, where you want to force the player to use specific strategies against certain enemies, and be completely unable to deal damage otherwise. Subtractive formulas work best with very low stat numbers and a slow stat growth, including HP. With higher numbers or quicker stat growth, a subtractive formula can quickly cause the player to become totally invincible if they grind just a few extra levels, or if they backtrack. If your game ends with players having more than about 200 or 300 HP at the final boss, you should consider adjusting your stats downward, though it's possible to make larger numbers work using some more complex math in the formula, or by strictly limiting the player's ability to grind/backtrack.
In a game where most of the player's survival comes from healing, or where characters have similar defense to each-other, you are more likely to want a divisive damage formula, so that the player never reaches the point where they stop taking damage and stop needing to heal. This type of system is excellent for games where party members are all about as strong as each-other. It's mandatory for any system where the player has a single "tank" character, since you want to ensure that the tank always takes damage. Against enemies, it makes a great deal of sense for games where the player fights a lot of battles against 2 or fewer enemies at a time, because the player characters who have the "wrong" damage type or element against a certain enemy, or who have a low attack stat, are still going to need to need to attack that enemy anyway. When creating the actual equation for a divisive damage formula, you should strongly consider adding a constant to the attacker's attack power, for example damage = (a.atk + 150 / b.def), or a not-quite-constant such as (a.atk + a.level / bdef). Doing so will help guarantee that every attack does damage, and also help prevent the player's first few stat points at levels 2 and 3 from from being absurdly effective. If you have a strong focus on skills, and few or no normal attacks, each skill can have a "skill power" that you use for this constant.
In some games you may want player skills and enemy skills to use two different damage formulas. If your game has recruitable enemies, or enemies using the same class system as the player, or any other kind of strong parallel between enemies and party members, I'd advise against this as it breaks the illusion. But in most games, players have equipment and enemies don't; players are meant to win and enemies aren't; enemies have elemental weaknesses and players don't. These kinds of differences can mean that it makes a lot of sense to give one side or the other a bonus of some kind in combat.
Subtractive defense is the kind you're using now. The target's defense, or some number based on their defense, such as sqrt(defense), is subtracted from the final damage.
Divisive defense is when the final damage is divided by some number based on the target's defense. For example, (a.atk * 10 / b.def) is a simple and common divisive damage formula.
The main difference between these two types of formulas is whether having high enough defense can cause an attacker to do 0 damage. In certain types of games, it may be desirable to use a subtractive formula for this reason, for example in games where HP is low and healing is difficult but positioning or elemental defense is used to prevent damage. It may also be desirable in games with a very strong focus on using the right element, where you want to force the player to use specific strategies against certain enemies, and be completely unable to deal damage otherwise. Subtractive formulas work best with very low stat numbers and a slow stat growth, including HP. With higher numbers or quicker stat growth, a subtractive formula can quickly cause the player to become totally invincible if they grind just a few extra levels, or if they backtrack. If your game ends with players having more than about 200 or 300 HP at the final boss, you should consider adjusting your stats downward, though it's possible to make larger numbers work using some more complex math in the formula, or by strictly limiting the player's ability to grind/backtrack.
In a game where most of the player's survival comes from healing, or where characters have similar defense to each-other, you are more likely to want a divisive damage formula, so that the player never reaches the point where they stop taking damage and stop needing to heal. This type of system is excellent for games where party members are all about as strong as each-other. It's mandatory for any system where the player has a single "tank" character, since you want to ensure that the tank always takes damage. Against enemies, it makes a great deal of sense for games where the player fights a lot of battles against 2 or fewer enemies at a time, because the player characters who have the "wrong" damage type or element against a certain enemy, or who have a low attack stat, are still going to need to need to attack that enemy anyway. When creating the actual equation for a divisive damage formula, you should strongly consider adding a constant to the attacker's attack power, for example damage = (a.atk + 150 / b.def), or a not-quite-constant such as (a.atk + a.level / bdef). Doing so will help guarantee that every attack does damage, and also help prevent the player's first few stat points at levels 2 and 3 from from being absurdly effective. If you have a strong focus on skills, and few or no normal attacks, each skill can have a "skill power" that you use for this constant.
In some games you may want player skills and enemy skills to use two different damage formulas. If your game has recruitable enemies, or enemies using the same class system as the player, or any other kind of strong parallel between enemies and party members, I'd advise against this as it breaks the illusion. But in most games, players have equipment and enemies don't; players are meant to win and enemies aren't; enemies have elemental weaknesses and players don't. These kinds of differences can mean that it makes a lot of sense to give one side or the other a bonus of some kind in combat.
Adding base damage does not make the game easier to balance, it just changes how the balance works. The base damage means skills becomes less effective as the game progresses. A skill with 60 base damage doubles in power when your strength is just 60, but only increases the power by 20% when your strength is 500. This can be compared to a skill that simple does 150% the damage of a standard attack, it will do so no matter where you are at the game.
So adding base damage is a good idea if you want the player to gradually replace their skills with stronger ones as they progress trough the game and a bad idea if you want the skills to remain useful. It does not however make the game easier or harder to balance.
First ask yourself how you want the game to be balanced. As already indicated, "are skills supposed to be replaced by stronger ones or will they remain useful trough the entire game?" is one question to ask yourself. Another is "are characters supposed to be able to reduce incoming damage to zero with sufficient armor and if yes, how hard is that supposed to be?"
Once you know how the game is supposed to be balanced, we can construct formulas which accomplishes that task as easily as possible.
So adding base damage is a good idea if you want the player to gradually replace their skills with stronger ones as they progress trough the game and a bad idea if you want the skills to remain useful. It does not however make the game easier or harder to balance.
First ask yourself how you want the game to be balanced. As already indicated, "are skills supposed to be replaced by stronger ones or will they remain useful trough the entire game?" is one question to ask yourself. Another is "are characters supposed to be able to reduce incoming damage to zero with sufficient armor and if yes, how hard is that supposed to be?"
Once you know how the game is supposed to be balanced, we can construct formulas which accomplishes that task as easily as possible.
Sorry for the late reply! Got busy testing every suggestion in this topic!
Yes! Players will have a lot of choices in this. Different answers for quest dialogue may reward them with different stats and so on. Stat-raising items are found frequently as well.
Infact we would love if skills could be replaced with stronger/more interesting versions of themselves in a way that players can only equip a set number of skills, but so far we haven't found a way to do so (any suggestions?)
No no, they don't all go up! Actually, quest rewards are often items which can be used to increase characters stats manually. If the player choses to do a quest in one way they might receive a Dextery+ item while doing the quest differently awards a Strength+ item.
Considering that we're using small numbers, a +1 Magick does a lot.
We tested this one extensively and indeed, for small numbers, it's not ideal, although I really wanted to go on with this formula.
The thing is, the first enemy was taking upwards to 15 damage from normal attacks at 2 defense while the second enemy was taking about 6~7 damage at just 3 defense. A single defense buff made them ridiculously tanky and impossible to deal with.
This kind of formula seems easier to plan, however it definitely doesn't work unless numbers are larger. A shame because this :
This was almost exactly what I wanted, though. Is there a way to set a minimum damage everything can do or something?
Players and enemies share some skills, which are gained from cards dropped by enemies. I guess this is the most complicated part of balancing since the easiest way would be to set the enemy skill to just deal a 25 - b.def or something and set individual skills for each enemy.
...I never thought about it that way. Indeed it puts everything in perspective.
But what if 60 strength is a stat you only get to at the end of the game? Every point would mean a lot less, but elemental buffs and debuffs would mean a lot more.
This would perhaps make it easier to balance, but less engaging to players, perhaps?
Right now we're doing very small base damage with full scalling for each skill, considering increasing that base damage with skills learned at later levels and such and perhaps increasing scalling multiplicatively, if the points are meaning less and less results. We don't want the 'if I put enough points on it, it may make a difference one day' mindset many RPGs (specially ARPGs such as Diablo) go for. We want each point to remain useful through the whole game.
author=RyaReisender
On the other hand, does the player even have a choice on what stat to increase?
Yes! Players will have a lot of choices in this. Different answers for quest dialogue may reward them with different stats and so on. Stat-raising items are found frequently as well.
author=RyaReisender
Putting skill damage formulas is more a matter of how you want your skills to be like. Should they always be useful from start to finish? Should they get gradually less useful until they are replaced by a stronger version of the spell?
Infact we would love if skills could be replaced with stronger/more interesting versions of themselves in a way that players can only equip a set number of skills, but so far we haven't found a way to do so (any suggestions?)
author=Marrend
Well, if stats only go up by completing quests, you might consider making certain quests improve certain stats as a method for players to tailor their characters. If they all go up, that's probably fine too.
No no, they don't all go up! Actually, quest rewards are often items which can be used to increase characters stats manually. If the player choses to do a quest in one way they might receive a Dextery+ item while doing the quest differently awards a Strength+ item.
author=Marrend
I think the question in regards to game-balance becomes how much stats go up, and exactly how many of these quests are mandatory.
Considering that we're using small numbers, a +1 Magick does a lot.
author=LockeZ
Divisive defense is when the final damage is divided by some number based on the target's defense. For example, (a.atk * 10 / b.def) is a simple and common divisive damage formula.
We tested this one extensively and indeed, for small numbers, it's not ideal, although I really wanted to go on with this formula.
The thing is, the first enemy was taking upwards to 15 damage from normal attacks at 2 defense while the second enemy was taking about 6~7 damage at just 3 defense. A single defense buff made them ridiculously tanky and impossible to deal with.
This kind of formula seems easier to plan, however it definitely doesn't work unless numbers are larger. A shame because this :
author=LockeZis something undesirable, I wanted that the least they could do was 1, but oh well.
The main difference between these two types of formulas is whether having high enough defense can cause an attacker to do 0 damage.
author=LockeZ
In a game where most of the player's survival comes from healing, or where characters have similar defense to each-other, you are more likely to want a divisive damage formula, so that the player never reaches the point where they stop taking damage and stop needing to heal. This type of system is excellent for games where party members are all about as strong as each-other. It's mandatory for any system where the player has a single "tank" character, since you want to ensure that the tank always takes damage.
This was almost exactly what I wanted, though. Is there a way to set a minimum damage everything can do or something?
author=LockeZ
In some games you may want player skills and enemy skills to use two different damage formulas.
Players and enemies share some skills, which are gained from cards dropped by enemies. I guess this is the most complicated part of balancing since the easiest way would be to set the enemy skill to just deal a 25 - b.def or something and set individual skills for each enemy.
author=Crystalgate
A skill with 60 base damage doubles in power when your strength is just 60, but only increases the power by 20% when your strength is 500.
...I never thought about it that way. Indeed it puts everything in perspective.
But what if 60 strength is a stat you only get to at the end of the game? Every point would mean a lot less, but elemental buffs and debuffs would mean a lot more.
This would perhaps make it easier to balance, but less engaging to players, perhaps?
Right now we're doing very small base damage with full scalling for each skill, considering increasing that base damage with skills learned at later levels and such and perhaps increasing scalling multiplicatively, if the points are meaning less and less results. We don't want the 'if I put enough points on it, it may make a difference one day' mindset many RPGs (specially ARPGs such as Diablo) go for. We want each point to remain useful through the whole game.
LockeZ

I'd really like to get rid of LockeZ. His play style is way too unpredictable. He's always like this too. If he ran a country, he'd just kill and imprison people at random until crime stopped.
5958
author=Nana707
Is there a way to set a minimum damage everything can do or something?
If you're using a divisive damage formula, there are a few different ways, each with slightly different side-effects:
1) If you just want a hard floor on damage you can build a conditional branch into the damage formula. If you're using the damage formula boxes on the skill page, the syntax x?y:z will work like a conditional branch meaning "if x, then y, otherwise z." So for example if you want the damage formula a.atk * 10 / b.def, but with a minimum of 50 damage, you could type a.atk*10/b.def > 50 ? a.atk*10/b.def : 50 to get that result.
However this will mean that at low attack stat values or high defense stat values, buffs and debuffs and new equipment will have absolutely no effect whatsoever, which means that your game is lying to the player in many situations. You should not really do this. It's bad design. I'm only listing it because it most closely matches what you asked.
2) If you just add +50 to the end of your damage formula then everything will do 50 more damage. This is a better method with fewer side-effects. If you do this, you probably shouldn't make this number very high, because it makes stats worth less at the beginning of the game. The higher it is, the less stats are worth at the beginning of the game, and the more they're worth later. This makes the player's first few upgrades and level ups feel kinda lame, and also makes grinding become more and more effective the more you do it (which is typically the opposite of how you want grinding to work).
You can directly undo this side-effect by applying an exponent between 0 and 1 to the attack and defense stats in the damage formula: for example by replacing a.atk and b.def in the damage formula with a.atk^0.9 and b.def^0.9. This will cause stats to have slightly dimininishing returns, which is more in line with how most games work. A low enough exponent like 0.5 will also sharply reduce the effectiveness of grinding extra levels.
Alternately you can just make things that increase the player's stats (such as level ups and new equipment) be high enough at the beginning of the game that the increases still feel worthwhile. Or you can just ignore this side-effect, since it's not necessarily "bad" unless the value is so high that a big chunk of the player's damage is coming from this.
3) You can use a logarithmic formula to make damage gradually approach a certain value as the attacker gets weaker and weaker or as the defender gets stronger and stronger, but this kind of formula won't fit in the skill database and you would need to use heavier scripting to achieve it. You'd also have to be good enough at math to do it yourself, since it would take a lot of fiddling to get it right. The end result would be something similar to method #2 but with a smoother curve.
4) If the strongest enemy's defense is 10x as high as a level 1 player's attack power, and a max level player's defense is 10x as high as the weakest enemy's attack power, then multiplying the attacker's attack power by any number higher than 10 will ensure that the player always does damage. 10x probably isn't the right number for your game, but some number is right - you can compare last-dungeon defense to first-dungeon attack power and figure out how big a number you need to multiply the damage by. However, if your game is long and the player and enemies' stats grow by a lot by the end of the game, this method will be impossible, because the multiplier will be so high that you'll need to give players and enemies a hundred thousand HP to survive attacks.
---
About how high are your players' and enemies' HP at the beginning of the game and at the end of the game? Based on that info I think I can probably give you a pretty reasonable damage formula based on what you've said you're doing and what you've said you want to be doing.
author=LockeZ
1) If you just want a hard floor on damage you can build a conditional branch into the damage formula. If you're using the damage formula boxes on the skill page, the syntax x?y:z will work like a conditional branch meaning "if x, then y, otherwise z." So for example if you want the damage formula a.atk * 10 / b.def, but with a minimum of 50 damage, you could type a.atk*10/b.def > 50 ? a.atk*10/b.def : 50 to get that result.
However this will mean that at low attack stat values or high defense stat values, buffs and debuffs and new equipment will have absolutely no effect whatsoever, which means that your game is lying to the player in many situations. You should not really do this. It's bad design. I'm only listing it because it most closely matches what you asked.
Unfortunately we're not using divisive damage formula because of low numbers, but we kinda wanted to.
We actually do use conditional damage of this sort of thing for specific moves that target status effects or some other things but in a general sense it feels too static indeed.
author=LockeZ
2) If you just add +50 to the end of your damage formula then everything will do 50 more damage. This is a better method with fewer side-effects. If you do this, you probably shouldn't make this number very high, because it makes stats worth less at the beginning of the game. The higher it is, the less stats are worth at the beginning of the game, and the more they're worth later. This makes the player's first few upgrades and level ups feel kinda lame, and also makes grinding become more and more effective the more you do it (which is typically the opposite of how you want grinding to work).
You can directly undo this side-effect by applying an exponent between 0 and 1 to the attack and defense stats in the damage formula: for example by replacing a.atk and b.def in the damage formula with a.atk^0.9 and b.def^0.9. This will cause stats to have slightly dimininishing returns, which is more in line with how most games work. A low enough exponent like 0.5 will also sharply reduce the effectiveness of grinding extra levels.
It's pretty cool to have a set precise number that will be in the formula disconsidering stats altogether. It does exactly what I wanted, never thought of that. Do you think it could work together with base damage, or if it's best to not have a base damage at all? Or if it's better to have something like: ((10+a.atk)-b.def)+5?
However, if so, this would cripple defensive buffs way too much and make offensive ones less effective.
Using atk^0.9 or another number, would it be possible to have a low stat divisible formula in which buffs and debuffs don't completely break the game? And if so how much should a buff or defuff increase or decrease? We're using 50% of the stats. Or would exponents just give the same results? For example a.atk^0.9 - b.def^0.8 or something? We're really bad at math here, sorry.
author=LockeZ
If the strongest enemy's defense is 10x as high as a level 1 player's attack power, and a max level player's defense is 10x as high as the weakest enemy's attack power, then multiplying the attacker's attack power by any number higher than 10 will ensure that the player always does damage. 10x probably isn't the right number for your game, but some number is right - you can compare last-dungeon defense to first-dungeon attack power and figure out how big a number you need to multiply the damage by. However, if your game is long and the player and enemies' stats grow by a lot by the end of the game, this method will be impossible, because the multiplier will be so high that you'll need to give players and enemies a hundred thousand HP to survive attacks.
---
About how high are your players' and enemies' HP at the beginning of the game and at the end of the game? Based on that info I think I can probably give you a pretty reasonable damage formula based on what you've said you're doing and what you've said you want to be doing.
>> At the beginning of the game, the first character's relevant stats are:
30 HP
5 ATK (initial weapon increases it to 12)
1 DEF (first equipment increases it to 3)
First enemy is
22 HP
5 ATK
2 DEF
We're 100% unsure how the last levels should look like, but I don't want them to go way too high, something like 500 HP at the last dungeon should be the highest I guess? But it's totally open right now. Since we're not using the stat growth curves from RPG maker to go with our own stat increasing items throught the game, this kind of thought becomes rather blurry.
LockeZ

I'd really like to get rid of LockeZ. His play style is way too unpredictable. He's always like this too. If he ran a country, he'd just kill and imprison people at random until crime stopped.
5958
It sounds like you like all the outcomes of the divisible defense formulas, but aren't sure how to make it work in a game where players and enemies start out with single-digit stats and maintain very low stats across the game.
Getting a formula that works at one point in the game is pretty easy, but without knowing how your stats progress, the only way I can really come up with something that works for your whole game is to tell you how your stats should progress with this damage formula. So, that's what I'll do, I suppose.
Some of these numbers are different than what I said before, mostly because it sounds like you want HP to increase a lot as the game goes on, and because you want attack power to be a higher number than defense power. However I think it should work pretty well.
Try this damage formula for normal attacks:
This'll mean that in your first battle in the game, the player will be doing 17-18 damage, and the enemy will be doing 9 damage. If you feel like this makes the enemy or player die too fast, try adjusting enemy and player stats before you start adjusting the formula.
Then for skills, you probably just want to add a multiplier. For example, a skill called Doublestrike that is twice as strong as a normal attack would have the formula:
For magical skills you can use the exact same formula, just use a.mat and b.mdf in place of a.atk and b.def.
With this kind of formula you probably want your player and enemy stats to grow sort of like this:
This formula with this plan won't give you a perfectly balanced game but I think it's a good starting point. Once you get started, it'll also make balance a lot easier on you, because you'll know exactly how much to increase enemy stats and equipment stats by in each dungeon, instead of having to test with thirty different numbers each time to find the right sweet spot.
Getting a formula that works at one point in the game is pretty easy, but without knowing how your stats progress, the only way I can really come up with something that works for your whole game is to tell you how your stats should progress with this damage formula. So, that's what I'll do, I suppose.
Some of these numbers are different than what I said before, mostly because it sounds like you want HP to increase a lot as the game goes on, and because you want attack power to be a higher number than defense power. However I think it should work pretty well.
Try this damage formula for normal attacks:
Math.pow(a.atk + 5, 1.5) / Math.pow(b.def + 5, 0.8) + 3
This'll mean that in your first battle in the game, the player will be doing 17-18 damage, and the enemy will be doing 9 damage. If you feel like this makes the enemy or player die too fast, try adjusting enemy and player stats before you start adjusting the formula.
Then for skills, you probably just want to add a multiplier. For example, a skill called Doublestrike that is twice as strong as a normal attack would have the formula:
2 * (Math.pow(a.atk + 5, 1.5) / Math.pow(b.def + 5, 0.8) + 3)
For magical skills you can use the exact same formula, just use a.mat and b.mdf in place of a.atk and b.def.
With this kind of formula you probably want your player and enemy stats to grow sort of like this:
- Around the time the player reaches the third dungeon, I'd expect the heroes and enemies both to have about twice as much attack and defense, and about 75% more HP, compared to the first dungeon. This includes stats from the player's equipment.
- Attack and defense should continue to increase at the same rate as each-other, and HP should continue to increase by about 75% every time att/def are doubled. This applies to both players and enemies.
- Once the player gets reliable healing spells that they can easily cast almost every round for a low cost, you should double enemy attack power for the rest of the game.
- Multiply the enemy HP by the number of party members. So when the player gets their second party member, enemies from that dungeon onward will have twice as much HP as before. When they get their third party member, enemies should start having another 50% more HP, to a total of triple the original amount.
- If the player starts with more than 1 party member, you should probably wait until the second dungeon to increase enemy stats, to be nice.
- By the end of the game, let's imagine that attack and defense have each doubled about five times. This would mean that player stats are likely to be something like 400 att, 100 def, and 500 HP. Enemy stats are likely to be something like 300 att, 65 def, and (350 x partymembers) HP. In this example situation, player attacks would do about 300 damage and enemy attacks would do about 150 damage. This is just an example though. Att/def might only double twice over the course of the game if it's a shorter game.
- Players don't need to gain defense from level ups at all. They should probably gain all their defense from equipment. Level ups can still provide attack power and HP though.
- Physical and magical stats should be about equal. If you want magical skills to be stronger, build that into the skill's multiplier.
- Bosses should generally have extra HP rather than extra defense, unless you want them to specifically be strong against only physical attacks or only magical attacks.
- Buffs and debuffs should be multipliers for stats, not additions. For example, a moderate attack power buff might give 25% bonus attack power. A moderate defense buff might give 50% bonus defense. (Both of these buffs are actually the same strength, and will cancel each-other out, because att and def have different exponents in the damage formula.)
This formula with this plan won't give you a perfectly balanced game but I think it's a good starting point. Once you get started, it'll also make balance a lot easier on you, because you'll know exactly how much to increase enemy stats and equipment stats by in each dungeon, instead of having to test with thirty different numbers each time to find the right sweet spot.
author=LockeZ
Try this damage formula for normal attacks:
Math.pow(a.atk + 5, 1.5) / Math.pow(b.def + 5, 0.8) + 3
This! This really, really, REALLY helps!
I've tried it and it does work prfectly for normal attacks and some abilities, with the added base damage and sometimes multiplying the whole thing.
I've noticed it also works really well on composite (?) formulas, such as for the Scythe's ability that goes like
a.gainHp(2 + a.mdf); 0.6 * (Math.pow(a.atk + a.mat + 12, 1.5) / Math.pow(b.def + 5, 0.8) + 2)
(correct me if I'm wrong but this, so far, seems to be working as intended. I've tested most abilities with varying amounts of stats going upwards to 100ish attack and the damage growths seem to be stable)
Thank you so much!
author=LockeZ
With this kind of formula you probably want your player and enemy stats to grow sort of like this:
This is possibly the best kind of guideline for balancing I've ever came across, you can be sure I'll follow this very closely. You should make it a guide or something, it's ABSURDLY helpful!
I had no idea how to make stuff stronger throught the game and how much should everything increase, but this made it so much easier. Thank you again.
Just one little thing
author=LockeZ
Buffs and debuffs should be multipliers for stats, not additions. For example, a moderate attack power buff might give 25% bonus attack power. A moderate defense buff might give 50% bonus defense.
Doesn't increasing attack by 25% only increase the final damage by far less than 25%? I'm not really good at math here so correct me if I'm wrong, it feels like a small increase.
PS: You're the best.
LockeZ

I'd really like to get rid of LockeZ. His play style is way too unpredictable. He's always like this too. If he ran a country, he'd just kill and imprison people at random until crime stopped.
5958
The composite formula seems... probably fine? At very high stat values you might find that it grows faster than other skills, but maybe not depending on your characters' stats. Depends how easy it is to build a hybrid character who has both stats at high numbers.
Specifically, to figure out how much, convert the percentage into a decimal, and then raise it to the power of 1.5. So for example, a buff that multiplies your attack power by 1.25, it's multiplying your damage by 1.25 ^ 1.5, which is 1.397 (a 39.7% increase in damage). If you had a debuff that halved your attack power, it would multiply your damage by 0.5 ^ 1.5, which is 0.356 (you'd do 35.6% as much damage as normal).
For defense buffs and debuffs, you calculate it the same way, except raise it to the power of 0.8 instead of 1.5. Because the exponent here is less than 1, a 1% change in defense is worth less than a 1% difference in damage, like how you were thinking attack power would work. For example, a buff that multiplied your defense by 1.5 would divide your damage taken by 1.5 ^ 0.8, which means it'd divide your damage taken by 1.383 (which is the same as multiplying your damage taken by 0.723, or by 72.3%). This almost perfectly cancels out the 25% buff in attack power from the first example.
Just as one extra note: If you start giving the player near-unlimited access to skills that deal, say, twice as much damage as a normal attack, you should probably start giving the enemies twice as much HP to compensate. I'm not necessarily sure the reverse is true if you start giving stronger skills to enemies though - player HP might still be fine depending on a variety of things like buffs and healing and the back row.
author=Nana707No, because the exponent is higher than 1. It's 1.5, so 1% of attack is worth more than 1% of damage.
Doesn't increasing attack by 25% only increase the final damage by far less than 25%? I'm not really good at math here so correct me if I'm wrong, it feels like a small increase.
Specifically, to figure out how much, convert the percentage into a decimal, and then raise it to the power of 1.5. So for example, a buff that multiplies your attack power by 1.25, it's multiplying your damage by 1.25 ^ 1.5, which is 1.397 (a 39.7% increase in damage). If you had a debuff that halved your attack power, it would multiply your damage by 0.5 ^ 1.5, which is 0.356 (you'd do 35.6% as much damage as normal).
For defense buffs and debuffs, you calculate it the same way, except raise it to the power of 0.8 instead of 1.5. Because the exponent here is less than 1, a 1% change in defense is worth less than a 1% difference in damage, like how you were thinking attack power would work. For example, a buff that multiplied your defense by 1.5 would divide your damage taken by 1.5 ^ 0.8, which means it'd divide your damage taken by 1.383 (which is the same as multiplying your damage taken by 0.723, or by 72.3%). This almost perfectly cancels out the 25% buff in attack power from the first example.
Just as one extra note: If you start giving the player near-unlimited access to skills that deal, say, twice as much damage as a normal attack, you should probably start giving the enemies twice as much HP to compensate. I'm not necessarily sure the reverse is true if you start giving stronger skills to enemies though - player HP might still be fine depending on a variety of things like buffs and healing and the back row.
I want to tip my hat to LockeZ for his work on formulas in this topic. Good stuff.
I also want to throw my hat in as well with an alternative formula. I'm not going to argue it's better than what LockeZ suggested, but it's different, so you may want to test it out.
a.atk^2/(a.atk+b.def)
The above formula was designed with simplicity and common sense in mind. To that end, it doesn't overreact with small changes and damage will always scale linearly with equal atk and def scaling. To better explain, let me give you some examples:
50% decrease in def doesn't mean a huge spike in damage.
12 atk against 3 def = 9.6 damage.
12 atk against 2 def, you do 10.3 damage.
The numbers scale cleanly, so you can easily figure out how much damage you'll be doing late game.
12 atk against 3 def = 9.6 damage.
1200 atk against 300 def = 960 damage.
A 50% increase in atk doesn't cause an insane damage spike either.
1200 atk against 300 def = 960 damage.
1800 atk against 300 def = 1543 damage.
Maximum damage always equals the atk value.
1000 atk against zero def = 1000 damage.
You can, however, become invincible with a lot of defense.
100 atk against 1000 def = 9 damage
In general, if atk = def, then damage = half of atk.
10 atk against 10 def = 5 damage.
420 atk against 420 def = 210 damage.
1000 atk against 1000 def = 500 damage.
Because the formula scales plainly as stats increase, it's relatively easy for you to know or guess how much damage something will do. This in turn allows you to properly set HP values based upon how many hits you want the monster to take before it is defeated. This also means that if you want random enemies to always take the same number of hits, you simply need to increase their HP the same percentage that atk is increased (so if atk is doubled, HP is doubled). And because the formula is resistant to small changes, it won't go all crazy on you if you make some small balancing errors.
It's not a perfect formula, but I find it works well if you want to try it out.
I also want to throw my hat in as well with an alternative formula. I'm not going to argue it's better than what LockeZ suggested, but it's different, so you may want to test it out.
a.atk^2/(a.atk+b.def)
The above formula was designed with simplicity and common sense in mind. To that end, it doesn't overreact with small changes and damage will always scale linearly with equal atk and def scaling. To better explain, let me give you some examples:
50% decrease in def doesn't mean a huge spike in damage.
12 atk against 3 def = 9.6 damage.
12 atk against 2 def, you do 10.3 damage.
The numbers scale cleanly, so you can easily figure out how much damage you'll be doing late game.
12 atk against 3 def = 9.6 damage.
1200 atk against 300 def = 960 damage.
A 50% increase in atk doesn't cause an insane damage spike either.
1200 atk against 300 def = 960 damage.
1800 atk against 300 def = 1543 damage.
Maximum damage always equals the atk value.
1000 atk against zero def = 1000 damage.
You can, however, become invincible with a lot of defense.
100 atk against 1000 def = 9 damage
In general, if atk = def, then damage = half of atk.
10 atk against 10 def = 5 damage.
420 atk against 420 def = 210 damage.
1000 atk against 1000 def = 500 damage.
Because the formula scales plainly as stats increase, it's relatively easy for you to know or guess how much damage something will do. This in turn allows you to properly set HP values based upon how many hits you want the monster to take before it is defeated. This also means that if you want random enemies to always take the same number of hits, you simply need to increase their HP the same percentage that atk is increased (so if atk is doubled, HP is doubled). And because the formula is resistant to small changes, it won't go all crazy on you if you make some small balancing errors.
It's not a perfect formula, but I find it works well if you want to try it out.
LockeZ

I'd really like to get rid of LockeZ. His play style is way too unpredictable. He's always like this too. If he ran a country, he'd just kill and imprison people at random until crime stopped.
5958
Yeah, that's a formula I've seen before in professional games, and it works well in a lot of games well for all the reasons you described. It does have a couple noteworthy side-effects though. First, it means that if the defender is significantly lower level, then buffing their defense is totally ineffective. And second, it means that if the attacker is significantly lower level, then buffing their attack power is crazy-ultra-effective.
That formula does give you very predictable damage when both sides' stats are about equal, and each side's attack and defense power are also about equal. But it behaves less nicely when one side is vastly more powerful than the other. In many RPGs, that's not a problem, because the player is always expected to be fighting enemies right around their own level, stronger enemies/areas are gated by story progression, and you don't particularly care what happens if they go back to early-game areas. But if you're making an open world game where gaining levels is a big part of the driving gameplay, and the player can fight enemies far above their own level for huge XP gains, then it's a bad fit because of how weirdly it behaves in that situation.
That formula does give you very predictable damage when both sides' stats are about equal, and each side's attack and defense power are also about equal. But it behaves less nicely when one side is vastly more powerful than the other. In many RPGs, that's not a problem, because the player is always expected to be fighting enemies right around their own level, stronger enemies/areas are gated by story progression, and you don't particularly care what happens if they go back to early-game areas. But if you're making an open world game where gaining levels is a big part of the driving gameplay, and the player can fight enemies far above their own level for huge XP gains, then it's a bad fit because of how weirdly it behaves in that situation.
I actually like how it behaves when there are vast level differences, since the damage cap keeps unexpectedly strong enemies from one-shotting you, even though it does open the door for some level of abuse.
-
I put together a list of a range of possible atk and def values and how three formula options behave. The first is LockeZ's formula. The second is the one I posted, but with some slight edits to make it a bit more comparable to LockeZ's formula with small numbers. The final is the pure, unedited formula. Hopefully this will help not only in making a decision (if you haven't already) but also in understanding the formula you're using.
Note that LockeZ designed his formula for unequal atk and def values, while mine is designed for equal atk and def values. Therefore the comparison isn't perfect. But hopefully there are enough examples listed that it's still useful.
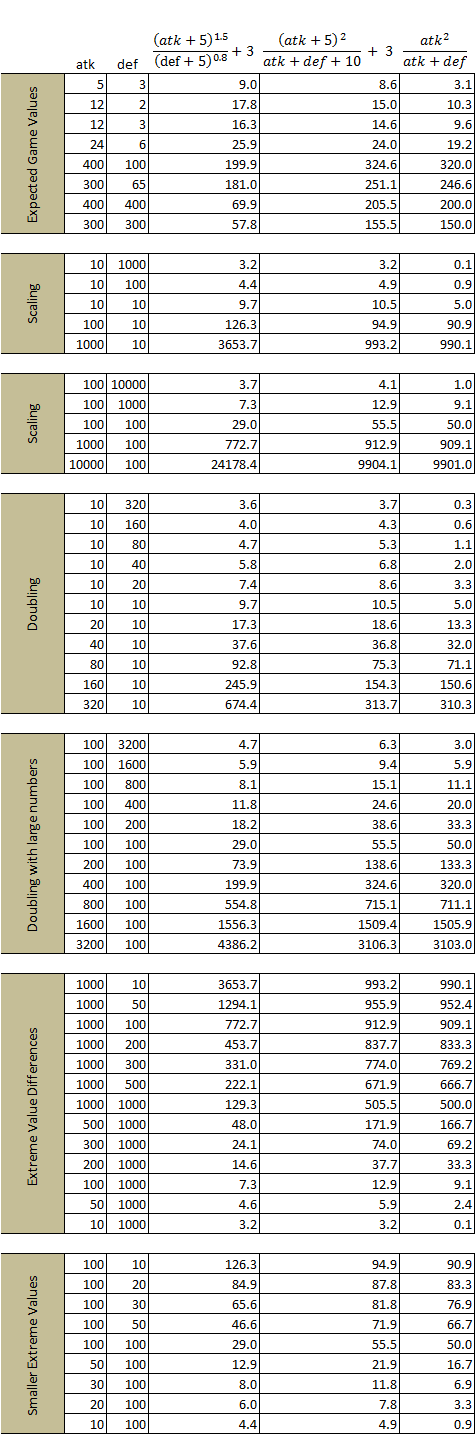
-
I put together a list of a range of possible atk and def values and how three formula options behave. The first is LockeZ's formula. The second is the one I posted, but with some slight edits to make it a bit more comparable to LockeZ's formula with small numbers. The final is the pure, unedited formula. Hopefully this will help not only in making a decision (if you haven't already) but also in understanding the formula you're using.
Note that LockeZ designed his formula for unequal atk and def values, while mine is designed for equal atk and def values. Therefore the comparison isn't perfect. But hopefully there are enough examples listed that it's still useful.

author=LockeZ
Yeah, that's a formula I've seen before in professional games, and it works well in a lot of games well for all the reasons you described. It does have a couple noteworthy side-effects though. First, it means that if the defender is significantly lower level, then buffing their defense is totally ineffective. And second, it means that if the attacker is significantly lower level, then buffing their attack power is crazy-ultra-effective.
Well, imagine we have two different encounters, one against a single giant with 600 attack and another against six goblins with 100 attack each. It does feel intuitive to me that armor would be more useful against multiple weak attacks than against a single massive strike. In some games you may also want buffing to be differently effective against different encounters. It gives the player something to take into account while also allowing for easily followed visual cues (this enemy looks really strong, so buffing defense will help relative little and that enemy wears heavy metallic armor, so buffing attack or going magic will help a lot). Of course, in other games you don't have that desire.
What is a side effect for one game can be the primary effect you're aiming for in another game.
Pages:
1


















